Machine Learning: Machine Learning is a branch of research that allows computers to “learn” in the same way that humans do without the use of explicit programming.
Predictive modelling is a probabilistic approach that allows us to foresee events based on a set of predictors. These predictors are essentially characteristics that are considered while determining the model’s final outcome. So join Machine Learning Course in Chennai to enhance your technical skills in Machine Learning.
What is Dimensionality Reduction?
There are frequently too many factors on which the final categorization is made in machine learning classification tasks. These elements are essentially variables known as features. The more features there are, the more difficult it is to visualise and then work on the training set. Most of these characteristics are sometimes linked and so redundant. Dimensionality reduction methods are useful in this situation. Dimensionality reduction is the process of reducing the number of random variables under consideration by establishing a set of primary variables. It is split into two parts: feature selection and feature extraction.
To learn more about dimensionality reduction techniques in data mining join Machine Learning Online Course at FITA Academy.
Why is Dimensionality Reduction Important in Machine Learning and Predictive Modeling?
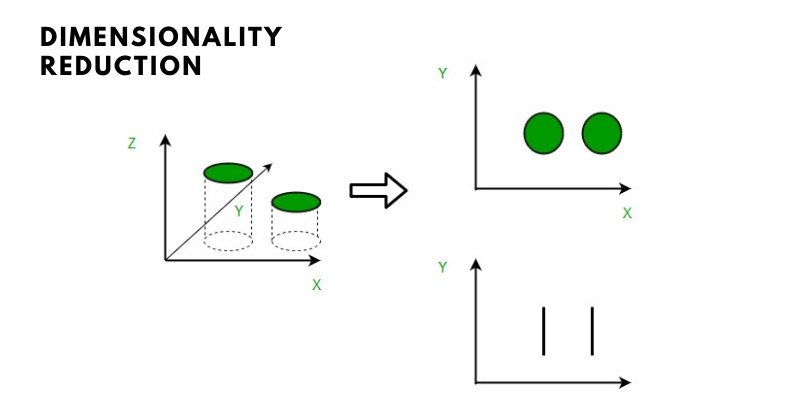
A simple e-mail classification problem, in which we must determine if the e-mail is spam or not, provides an intuitive illustration of dimensionality reduction. This can include a variety of factors, such as whether the email has a generic subject, the email’s content, whether the email employs a template, and so on. Some of these characteristics, however, may overlap. In another case, a classification problem including both humidity and rainfall can be simplified to simply one underlying feature due to their strong correlation. As a result, the number of features in such situations can be reduced. A 3-D classification problem can be difficult to picture, but a 2-D problem can be mapped to a basic two-dimensional space, and a 1-D problem to a simple line. This idea is demonstrated in the picture below, in which a 3-D feature space is split into two 1-D feature spaces, and the number of features can be reduced even further if they are discovered to be related.
Dimensionality reduction is made up of two parts:
- Feature selection: Here, we strive to locate a subset of the original collection of variables, or features, in order to reduce the number of variables that can be utilised to describe the problem. It usually takes three forms:
- Filter
- Wrapper
- Embedded
- Feature extraction: Feature extraction reduces data from a high-dimensional space to a lower-dimensional space, or one with fewer dimensions.
Dimensionality Reduction Techniques
The following are some of the dimensionality reduction techniques:
- Principal Component Analysis (PCA)
- Linear Discriminant Analysis (LDA)
- Generalized Discriminant Analysis (GDA)
Dimensionality reduction might be linear or non-linear, depending on the approach used. Linear Discriminant Analysis (LDA) Generalized Discriminant Analysis (GDA) The principal linear approach, often known as Principal Component Analysis, or PCA, is explored further down.
Principal Component Analysis
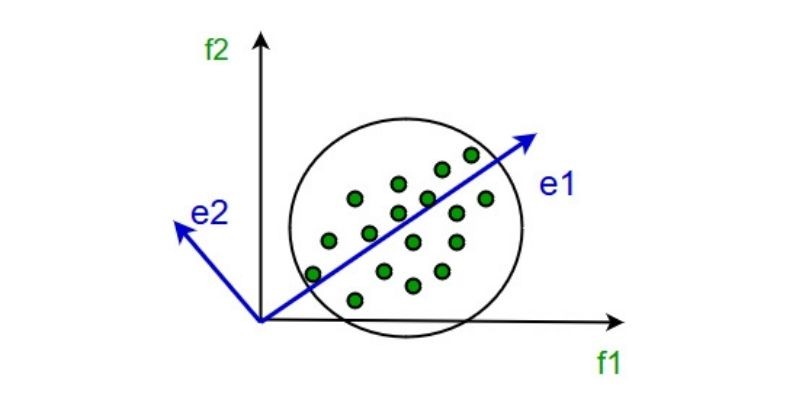
Karl Pearson pioneered this technique. It works on the premise that when data from a higher dimensions space is translated to data from a lower dimensional space, the lower dimensional space’s variance should be the greatest.
It Entails The Following Procedures:
- Construct the data’s covariance matrix.
- Calculate the matrix’s eigenvectors.
- To recover a large fraction of the variance of the original data, eigenvectors corresponding to the biggest eigenvalues are used.
As a result, we have a smaller number of eigenvectors, and some data may have been lost in the process. However, the remaining eigenvectors should keep the most significant variances.
Conclusion:
So far we have discussed about what is dimensionality reduction and dimensionality reduction in machine learning. So join Machine Learning course in Bangalore to learn more about Why Should We Learn Machine Learning? and dimensionality reduction techniques.